Lecture 4: Floats & Random Numbers¶

Date: 09/12/2017, Tuesday

In [1]:

format compact
format long % print more digits

Floating point number system¶

Double precision:

\[\begin{split}x = \pm(1+f)2^e \\ 0 \le 2^{t}f<2^{t}, t=52 \\ -1022 \le e \le 1023\end{split}\]

(See lecture slides or textbook for more explantion. This website focuses on codes.)

About parameters¶

How many binary bits are needed to store \(e\):

In [2]:

log2(2048)

ans =
    11

Maximum value¶

Calculate the maximum value of \(x\) from the formula.

In [3]:

t=52;
f=(2^t-1)/2^t;
(1+f)*2^1023

ans =
    1.797693134862316e+308

Compare with the built-in function

In [4]:

realmax

ans =
    1.797693134862316e+308

What happens if the value exceeds realmax?

In [5]:

2e308

ans =
   Inf

Minimum (absolute) value¶

From the formula

In [6]:

2^-1022

ans =
    2.225073858507201e-308

Compare with the built-in function

In [7]:

realmin

ans =
    2.225073858507201e-308

MATLAB allows you to go lower than realmin, but no too much.

In [8]:

for k=-321:-1:-325
    fprintf('k = %d, 10^k = %e \n',k,10^k)
end

k = -321, 10^k = 9.980126e-322
k = -322, 10^k = 9.881313e-323
k = -323, 10^k = 9.881313e-324
k = -324, 10^k = 0.000000e+00
k = -325, 10^k = 0.000000e+00

\(10^{-323}\) can be scaled up:

In [9]:

1e-323 * 1e300

ans =
     9.881312916824931e-24

But \(10^{-324}\) can’t, as it becomes exactly 0.

In [10]:

1e-324 * 1e300

ans =
     0

Machine precision¶

Compute machine precision¶

From the formula \(0 \le 2^{t}f<2^{t}, t=52\)

In [11]:

2^(-52)

ans =
     2.220446049250313e-16

Built-in function:

In [12]:

eps

ans =
     2.220446049250313e-16

Another ways to get eps

In [13]:

1.0-(0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1+0.1) % equals to eps/2

ans =
     1.110223024625157e-16

In [14]:

7/3-4/3-1 % equals to eps

ans =
     2.220446049250313e-16

Difference between eps and realmin¶

realmin is about abosolute magnitude, while eps is about relative accuracy. Although a double-precision number can represent a value as small as \(10^{-323}\) (i.e. realmin), the relative error of arithmetic operations can be as large as \(10^{-16}\) (i.e. eps).

Adding \(10^{-16}\) to 1.0 has no effect at all.

In [15]:

1.0+1e-16-1.0

ans =
     0

Adding \(10^{-15}\) to 1.0 has some effect, although the result is quite inaccurate.

In [16]:

1.0+1e-15-1.0

ans =
     1.110223024625157e-15

Not a number¶

In [17]:

0/0

ans =
   NaN

In [18]:

Inf - Inf

ans =
   NaN

However, Inf can sometimes be meaningful: (MATLAB-only. Not true in low-level languages.)

In [19]:

5/Inf

ans =
     0

In [20]:

5/0

ans =
   Inf

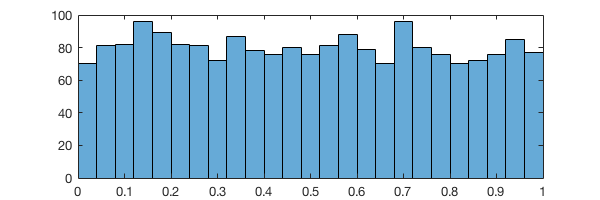
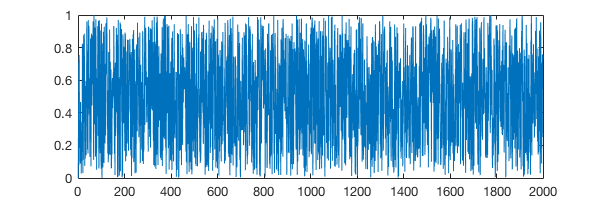
Random numbers¶

Linear congruential generator

In [21]:

a = 22695477;
c = 1;
m = 2^32;
N = 2000;

X = zeros(N,1);
X(1) = 1000;
for j=2:N
    X(j)=mod(a*X(j-1)+c,m);
end

R = X/m;

Hmm… looks pretty random🤔

In [22]:

%plot --size 600,200
plot(R);

The data also looks like evenly-distributed.

In [23]:

nbins = 25;
histogram(R, nbins);