Lecture 6: Matrix¶

Date: 09/19/2017, Tuessday

In [1]:

format compact

Matrix operation basics¶

Making a magic square

In [2]:

A = magic(3)

A =
     8     1     6
     3     5     7
     4     9     2

Take transpose

In [3]:

A'

ans =
     8     3     4
     1     5     9
     6     7     2

Rotate by 90 degree. (Not so useful for linear algebra. Could be useful for image processing.)

In [4]:

rot90(A')

ans =
     4     9     2
     3     5     7
     8     1     6

Sum over each column

In [5]:

sum(A)

ans =
    15    15    15

Another equivalent way

In [6]:

sum(A, 1)

ans =
    15    15    15

Sum over each row

In [7]:

sum(A, 2)

Extract the diagonal elements.

In [8]:

diag(A)

The sum of diagonal elements is also 15, by the definition of a magic square.

In [9]:

sum(diag(A))

ans =
    15

Determinant

In [10]:

det(A)

ans =
  -360

Matrix inversion \(A^{-1}\)

In [11]:

inv(A)

ans =
    0.1472   -0.1444    0.0639
   -0.0611    0.0222    0.1056
   -0.0194    0.1889   -0.1028

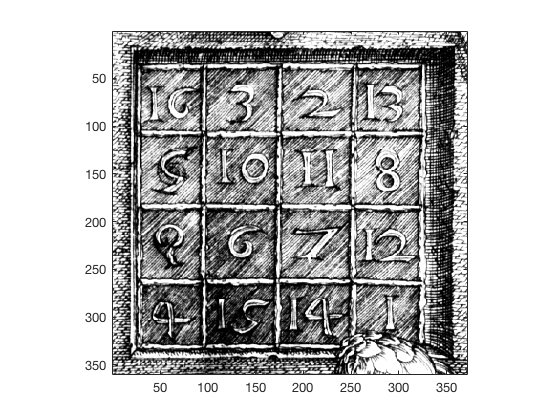
Built-in image for magic square¶

In [12]:

load durer
image(X)
colormap(map)
axis image

In [13]:

load detail
image(X)
colormap(map)
axis image

Vector norms¶

In [14]:

x = 1:5 % make a boring vector

x =
     1     2     3     4     5

Calculate p-norm from formula

In [15]:

my_norm = @(x,p) (sum(abs(x).^p))^(1/p)

my_norm =
  function_handle with value:
    @(x,p)(sum(abs(x).^p))^(1/p)

Check if it works.

In [16]:

my_norm(x,1)

ans =
    15

As p increases, the norm converges to \(\max(|x|)\)

In [17]:

for p=1:10
    my_norm(x,p)
end

ans =
    15
ans =
    7.4162
ans =
    6.0822
ans =
    5.5937
ans =
    5.3602
ans =
    5.2321
ans =
    5.1557
ans =
    5.1073
ans =
    5.0756
ans =
    5.0541

It blows up at \(p=442\) because \(5^{442}\) exceeds the realmin.

In [18]:

my_norm(x,441), my_norm(x,442)

ans =
     5
ans =
   Inf

In [19]:

5^441

ans =
  1.7611e+308

In [20]:

5^442

ans =
   Inf

Built-in function norm works for large numbers, though. Think about why.

In [21]:

norm(x,441), norm(x,442)

ans =
     5
ans =
     5

Conditioning¶

4x4 magic square

In [22]:

B = magic(4)

B =
    16     2     3    13
     5    11    10     8
     9     7     6    12
     4    14    15     1

It is singular and ill-conditioned.

In [23]:

inv(B)

Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND =  4.625929e-18.
ans =
   1.0e+15 *
   -0.2649   -0.7948    0.7948    0.2649
   -0.7948   -2.3843    2.3843    0.7948
    0.7948    2.3843   -2.3843   -0.7948
    0.2649    0.7948   -0.7948   -0.2649

In [24]:

det(B)

ans =
   5.1337e-13

In [25]:

cond(B)

ans =
   4.7133e+17

Use 1-norm instead. All norms should have similar order of magnitude.

In [26]:

cond(B,1)

Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND =  4.625929e-18.
> In cond (line 46)
ans =
   2.1617e+17

The condition number reaches 1/eps, leading to large numerical error.

In [27]:

1/eps

ans =
   4.5036e+15

Sparse matrix¶

In [28]:

A = eye(10)

A =
     1     0     0     0     0     0     0     0     0     0
     0     1     0     0     0     0     0     0     0     0
     0     0     1     0     0     0     0     0     0     0
     0     0     0     1     0     0     0     0     0     0
     0     0     0     0     1     0     0     0     0     0
     0     0     0     0     0     1     0     0     0     0
     0     0     0     0     0     0     1     0     0     0
     0     0     0     0     0     0     0     1     0     0
     0     0     0     0     0     0     0     0     1     0
     0     0     0     0     0     0     0     0     0     1

Store it in the sparse form saves memory.

In [29]:

As = sparse(A)

As =
   (1,1)        1
   (2,2)        1
   (3,3)        1
   (4,4)        1
   (5,5)        1
   (6,6)        1
   (7,7)        1
   (8,8)        1
   (9,9)        1
  (10,10)       1

Use whos A and whos As to check memory usage.

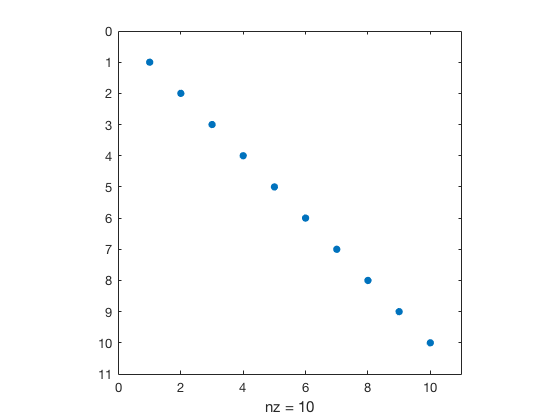
Visualize sparsity. Also works for As

In [30]:

spy(A)